Post Google Summer Of Code 2017

My GSoC 2017 project was to implement a package for Julia to solve Ordinary Differential Equations using Neural Networks. The purpose of the project was to provide an additional DE solver using Neural Networks which have a few parallelism and generalization advantages over other solvers. The project was based on a research paper which proposed the function approximation capabilities of Neural Networks for solving differential equations. The project was a mixture of research as well as implementation aspects and still has a few parts left to work upon. I chose to work on this project as I have interest in Mathematics and Machine Learning and it involved concepts of both the fields. The package uses DifferentialEquations.jl for the solver interface and KNet.jl for NN solver implementation.

How to use Neural Network for solving Differential Equations?

The concept of this solver is based on the UAT (Universal Approximation Theorem) which says that a Neural Network with not more than 3 hidden can approximate any continuous function. The Neural Network is made to minimize a loss function which then results in the convergence of our Trial solution towards the actual (analytical) solution. To know more about UAT click here.

Research aspect of the project and The Challenge

The research paper we referred on the topic is quite old and lacks proper explanation as well as examples. The research done on this part of Neural Networks is not too much and we were not able to get much help from the research papers related to the topic. The initial task was to read and understand the mathematics behind solving Differential Equations. Also the (analytical) methods used to solve Differential Equations on computers are quite different from the ones we use on paper so it took quite some time to get familiar with them. Also the structure and type of NN to be used so that the solver advantages are retained without compromising the performance was a research subdomain as well as a challenge.

Also after implementing the solver for ODEs (Ordinary Differential Equations) and System of ODEs the difficult part was to make the Neural Network converge, especially for the system of ODEs. As there are a lot of factors involved in Neural Networks like Hidden Layer Width, Number of Hidden Neurons, Activations, Weights etc., I relied on my Machine Learning background as well as the help from my mentors to experiment with most of the feasible settings of NN hyper-parameters and recording the accuracy of convergence and performance of the solver.

Making NN converge for System of ODEs is not as easy as it seems and took up most of the time for experimentation and tuning. Predicting the system of DEs solution with larger domain is still a challenge which needs to be worked upon.

Implementation and Work

Implementation involved integration of Mathematical and Machine Learning aspects through programming and to build a solver for ODEs. The DiffEqBase library is used as a base to extend the Algorithm and solver interface. The work done till now can be seen on the github repository primarily in this branch. This work involves implementing a Neural Network solver for ODEs with customized iterpolation based on NN prediction. The solver also works for system of ODEs but needs to be optimized for larger domains.

How does it work?

We need to construct a trial solution for our Differential Equation in terms of the NN output which should also satisfy the DE boundary conditions.
We define a loss function for the Neural Network which is same as equating the Differential to zero and minimizing that function (closer to 0 better convergence) wuth the trial solution substituted in it in place of the original function (or the solution to the DE). The Neural Network uses Adam optimization algorithm for backpropagation to tune its weights. GPU operation is supported by using the KnetArray type (the arry type used in KNet.jl) instead of regular Array for parameters and data, but requires CUDNN driver installed to access GPU hardware.

Examples

Below you can find a few examples on how to use the package I’ve been working on. Following are the initial imports required for the package to work.

using NeuralNetDiffEq
using Plots; plotly()
using DiffEqBase, ParameterizedFunctions
using DiffEqProblemLibrary, DiffEqDevTools
using Knet

ODE Examples

Example 1

  linear = (t,u) -> (1.01*u)
  (f::typeof(linear))(::Type{Val{:analytic}},t,u0) = u0*exp(1.01*t)
  prob = ODEProblem(linear,1/2,(0.0,1.0))
  sol = solve(prob,nnode(10),dt=1/10,iterations=10)
  plot(sol,plot_analytic=true)

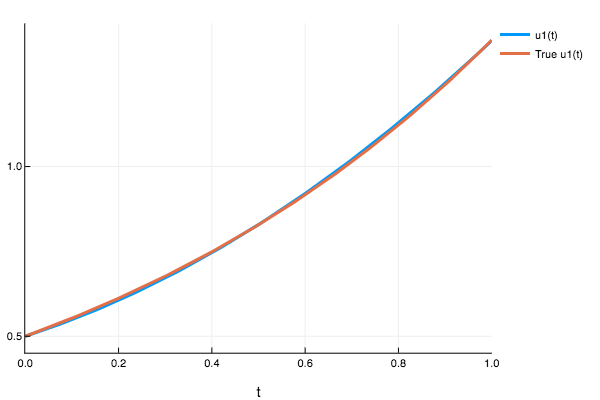
  sol(0.232)

  1-element Array{Any,1}:
   0.625818 #### Example 2

f = (t,u) -> (t^3 + 2*t + (t^2)*((1+3*(t^2))/(1+t+(t^3))) - u*(t + ((1+3*(t^2))/(1+t+t^3))))
(::typeof(f))(::Type{Val{:analytic}},t,u0) =  u0*exp(-(t^2)/2)/(1+t+t^3) + t^2
prob2 = ODEProblem(f,1.0,(0.0,1.0))
sol2 = solve(prob2,nnode(10),dt=0.1,iterations=200)
 plot(sol,plot_analytic=true)

  sol(0.47)

  1-element Array{Any,1}:
   0.803109

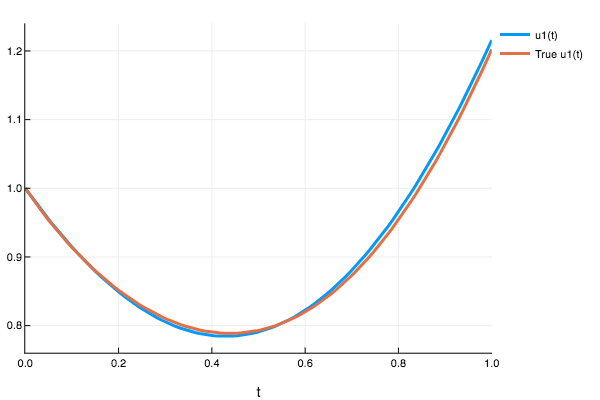
Example 3

f2 = (t,u) -> (-u/5 + exp(-t/5).*cos(t))
(::typeof(f2))(::Type{Val{:analytic}},t,u0) =  exp(-t/5)*(u0 + sin(t))
prob3 = ODEProblem(f2,Float32(0.0),(Float32(0.0),Float32(2.0)))
sol3 = solve(prob3,nnode(10),dt=0.2,iterations=1000)
 plot(sol,plot_analytic=true)

  sol3([0.721])

  1-element Array{Any,1}:
    Any[0.574705]

SODE Examples

Example 1 ODE 2D Linear

f_2dlinear = (t,u) -> begin
    du = Array{Any}(length(u))
    for i in 1:length(u)
    du[i] = 1.01*u[i]
  end
    return du
end
(f::typeof(f_2dlinear))(::Type{Val{:analytic}},t,u0) = u0*exp.(1.01*t)
prob_ode_2Dlinear = ODEProblem(f_2dlinear,rand(4,1),(0.0,1.0))
sol1 = solve(prob_ode_2Dlinear,nnode([10,50]),dt=0.1,iterations=100)

(:iteration,100,:loss,0.004670103680503722)
 16.494870 seconds (90.08 M allocations: 6.204 GB, 5.82% gc time)

plot(sol1,plot_analytic=true)

Example 2 Lotka Volterra

function lotka_volterra(t,u)
  du1 = 1.5 .* u[1] - 1.0 .* u[1].*u[2]
  du2 = -3 .* u[2] + u[1].*u[2]
  [du1,du2]
end

lotka_volterra (generic function with 1 method)

prob_ode_lotkavoltera = ODEProblem(lotka_volterra,Float32[1.0,1.0],(Float32(0.0),Float32(1.0)))
sol2 = solve(prob_ode_lotkavoltera,nnode([10,50]),dt=0.2,iterations=1000)

(:iteration,100,:loss,0.020173132003438572)
(:iteration,200,:loss,0.005130137452114811)
(:iteration,300,:loss,0.004812458584875589)
(:iteration,400,:loss,0.010083624565714974)
(:iteration,500,:loss,0.0025328170079611887)
(:iteration,600,:loss,0.007685579218433846)
(:iteration,700,:loss,0.005065291031504465)
(:iteration,800,:loss,0.005326863832044214)
(:iteration,900,:loss,0.00030436474139241827)
(:iteration,1000,:loss,0.0034853904995959094)
 22.126081 seconds (99.65 M allocations: 5.923 GB, 5.21% gc time)

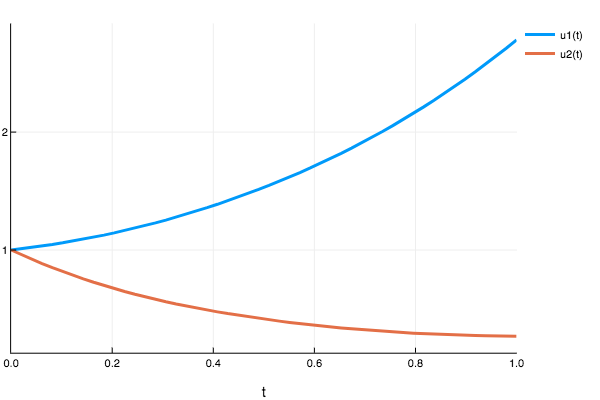
plot(sol2)

To see more examples and experiment results you can check out my Jupyter notebooks here.

Future Work

A bit more of research on the NN used as how it can be optimized for speed and better convergence. An optimization algorithm can be used for one time NN hyperparameter optimization so that it can work better for System of ODEs.

Acknowledgements

I would really want to thank my GSoC mentors Chris Rackauckas and Lyndon White for the help they provided in understanding mathematical as well as coding parts of the project. Also I would like to thank the Julia community in general for giving me opportunity to contribute and for sponsering my JuliaCon 2017 trip which was awesome.